数据表示及运算
数据的机器级表示
信息的二进制编码
自信息量:$I(x_i) = -log_2\:p(x_i)$
系统的信息熵:$H(X) = E[I(X)] = -\sum_i p(x_i)log_2p(x_i)$
补码
计算机中普遍使用补码
补码无论同号还是异号都可以直接相加
- 原码可能会出错
负数的补码等于对应的正数各位取反末位加一
浮点数二进制表示
科学计数法:$\pm S \times B^E$
- S:尾数
- B:基底
- E:阶码
规格化数
| S | E | M |
|---|---|---|
尾数(S)第一位总是1,不需要存于尾数字段(默认)
- 23位原码表示24位尾数
阶码(E)的真实值加偏移量后再存入阶码字段
真实值 -127~128
全0和全1表示特殊值
- 规格化数的阶码范围为0000 0001(-126) ~ 1111 1110(127)
规格化表示:
$\pm 1.bbb…b \times 2^E$
$X = (-1)^S \times M \times 2^E$
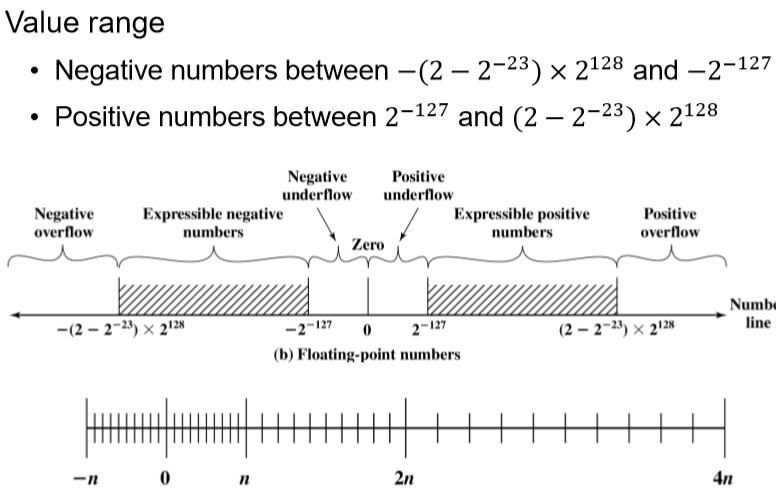
规格化数的范围:(重要难耐)
| 格式 | 最小整数 | 最大整数 | 最小负数 | 最大负数 |
|---|---|---|---|---|
| 单精度 | E = 1, M=0 | E = 254, M = $1 - 2^{-23}$ | E = 254, M = $1-2^{-23}$ | E = 1, M = 0 |
| 真值 | $1.0 \times 2^{-126}$ | $(2-2^{-23}) \times 2^{127})$ | $-(2-2^{-23}) \times 2^{127}$ | $-1.0 \times 2^{-126}$ |
| 阶码的值 | 尾数的值 | 表示 |
|---|---|---|
| 0(全0) | 0 | $\pm 0$ |
| 0(全0) | 非0 | 非规格化数 |
| 1~254 | 任意 | 规格化数 |
| 255(全1) | 0 | $\pm \infty$ |
| 255(全1) | 非0 | NaN |
非规格化数
用于处理规格化数中的下溢情况
$(-1)^S \times 0.bbb…b \times 2^{-126}$
自然BCD码(NBCD,8421码)(随便看看得了)
用四个二进制位表示每一个十进制数字
符号:四个最高有效位
- 正:1100
- 负:1101
数据校验码
纠错
基本思想:存储额外的信息以进行检错和校正
处理过程:
数据输入:使用函数f在M位数据D上生成K位校验码C
数据输出:使用函数f在M位数据$D’$上生成新的K位校验码$C’’$,并与取出的K位校验码$C’$进行比较
没有检测到差错:使用数据$D’$
检测到差错并可以校正:校正数据$D’$来生成数据$D’’$,并用数据$D’’$
检测到差错但无法纠正:报告
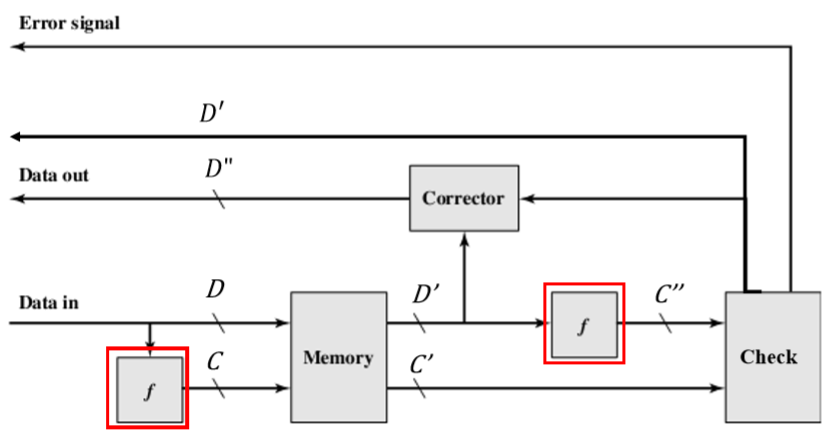
- 一旦进入Memory,C和D就已经永远消失了
奇偶校验码
增加1位校验码在数据最后面来表示数据中的1的数量是奇数还是偶数
处理过程:
假设数据为$D = D_M \cdots D_2 D_1$
数据输入
奇校验:$C = D_M \oplus \cdots D_2 \oplus D_1 \oplus 1$
偶校验:$C = D_M \oplus \cdots D_2 \oplus D_1$
数据输出
奇校验:$C’’ = D’_M \oplus \cdots D’_2 \oplus D’_1 \oplus 1$
偶校验:$C’’ = D’_M \oplus \cdots D’_2 \oplus D’_1$
检错
$S = C’’ \oplus C’$
S = 0:正确/数据中出错的位数为偶数
S = 1:数据中出错的位数为奇数
优点:代价低,只需要1位额外数据
缺点:不能发现出错位数为偶数的情形,发现错误后无法校正
海明码
将数据分成几组,对每一组都使用奇偶校验码进行检错
处理过程 :
将𝑀位数据分成𝐾组
数据输入:
- 为数据𝐷中每组生成1位校验码,合并得到𝐾位校验码𝐶
数据输出:
- 为数据𝐷′中每组生成1位校验码,合并得到新的𝐾位校验码𝐶′′
检错:将校验码𝐶′′和取出的校验码 C’ 按位进行异或,生成𝐾位故障字(syndrome word)
检验码
检验码的长度为 $2^K \geq M + K + 1$,使K成立的最小值就是校验码的位数
数据中有1位出现错误:M
检验码中有1位出现错误:K
没有出现错误:1
每一个检验位都放在二进制串中$2^n(n \in \mathbb{N})$的位置
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数据位 | $D_1$ | $D_2$ | $D_3$ | $D_4$ | $D_5$ | $D_6$ | $D_7$ | $D_8$ | ||||
| 校验位 | $C_1$ | $C_2$ | $C_3$ | $C_4$ |
检验位$C_i$负责检验二进制第 i 位为1的位置的检错
比如$C_1$负责0011、0101、0111 、1001$\cdots$,也就是第3、5、7、9 $\cdots$位
比如$C_2$负责0011、0110、0111、1010 $\cdots$,也就是第3、6、7、10$\cdots$位
检验位$C_i$的值要根据选择的奇/偶校验来决定
- 所有负责的位进行异或(奇检验最后还要异或1)
故障字
每种取值反映一种情形
全0:没有检测到错误
有且仅有1位是1:错误发生在校验码中的某一位,不需要纠正
有多位为1:错误发生在数据中的某一位,将$D’$中对应数据位取反即可纠正
| 故障字 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数据位 | $D_1$ | $D_2$ | $D_3$ | $D_4$ | $D_5$ | $D_6$ | $D_7$ | $D_8$ | ||||
| 校验位 | $C_1$ | $C_2$ | $C_3$ | $C_4$ |
循环冗余检测
- 模2运算:进行加法和减法都不进位
循环冗余检测CRC计算:假定数据M有k个比特,CRC运算就是在数据M后面添加供差错检测用的n位冗余码,然后构成一个帧发出去,一共发送(k + n)位
n位冗余码获得方式:在M后面加上n个0,得到的(n + k)位的数初一事先商定的(n + 1)位除数P,得出商是Q而余数是R(n位),这个余数R就作为冗余码拼接在数据M后面发送出去,也就是发送(k + n)位的CRC码
- 这种冗余码称作帧检验序列FCS(Frame Check Sequence)
接收端把收到的数据进行CRC检验:把收到的每一个帧除以相同的除数P(模2运算),然后检查得到的余数R
R = 0则判定没有差错,接收
R $\ne$ 0则出现差错(无法确定具体位置)
整数运算
加法
溢出表示:

全加器
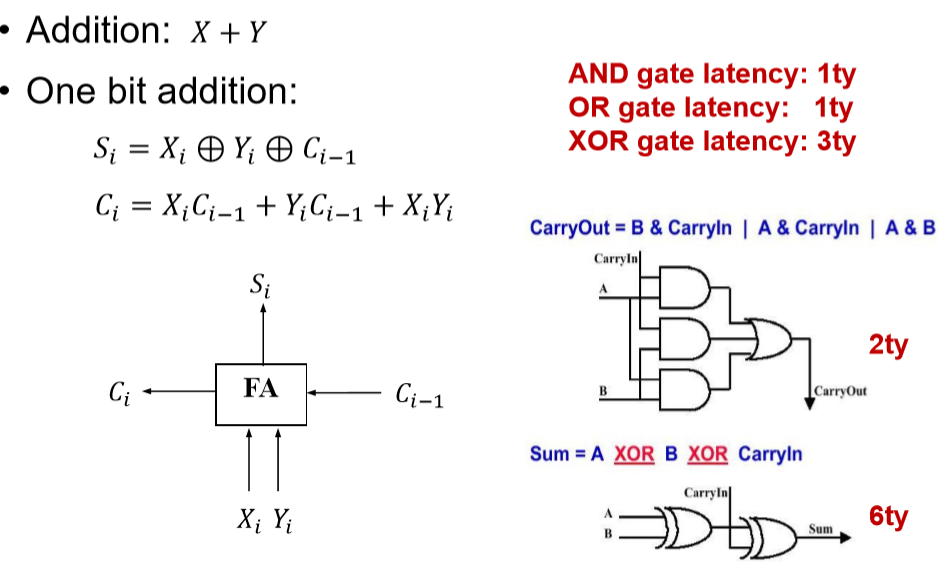
与门延迟:1ty ,或门延迟:2ty,异或门延迟:3ty
进位延迟:2ty,数据延迟:6ty
串行进位加法器
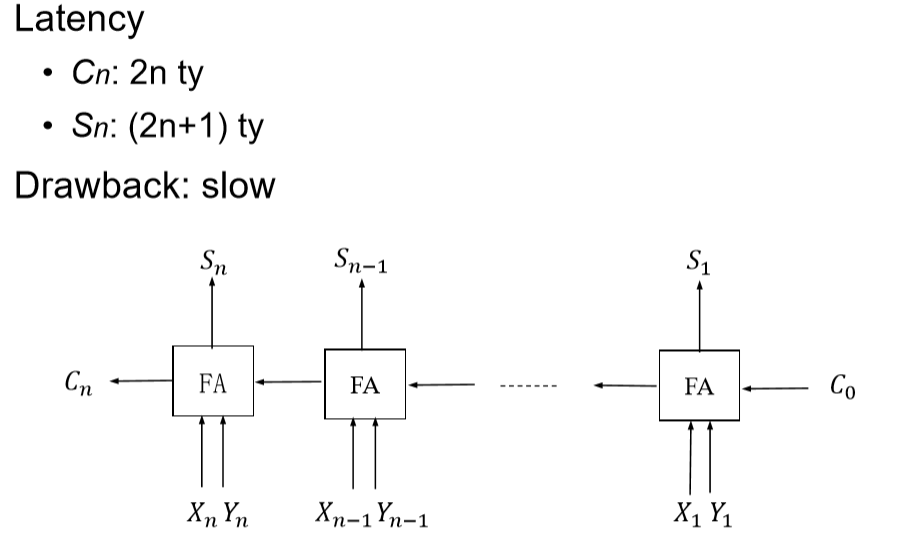
$S_n = 2 \times(n - 1) + 3 = 2n + 1$
在等待C来的时候,已经提前把$X_i$和$Y_i$进行计算
n=1的时候,计算出来是3,而实际是6
- 需要 $2 \times (n - 1) \geq 3$ 才行
$S_1 = 6,S_2 = 6,S_3 = 7$,$S_1$和$S_2$是同时出来的,只要C过去了就行
全先行进位加法器
超前进位:

所有的 $P_i$ 和 $G_i$ 都是可以同时计算的,代价是1ty
求出所有 $C_i$ 代价为2ty
- 先计算所有的与,再计算所有的或
求出所有的 $S_i$ 代价为3ty
异或只需要再做一次(有一次跟上面的时间重叠了)
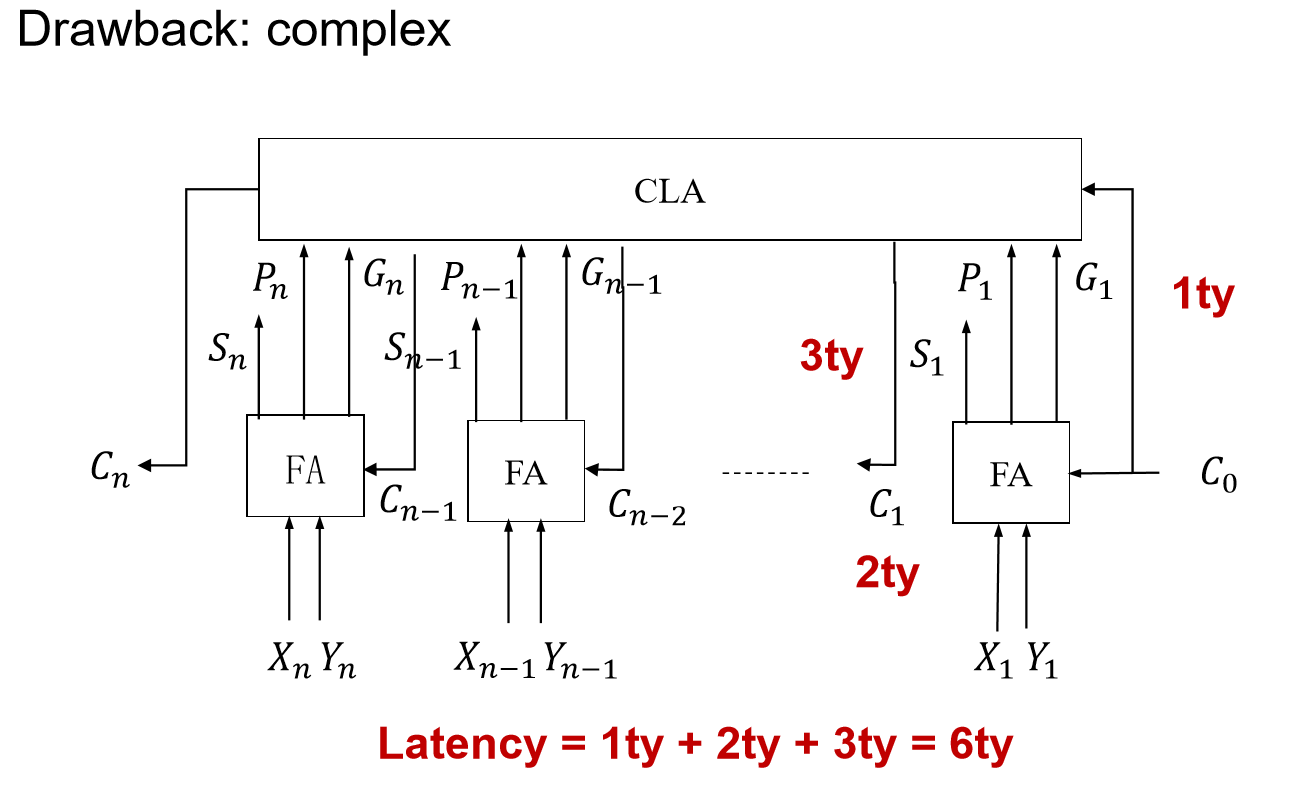
部分先行进位加法器
思路:采用多个CLA并将其串联,取得计算时间和硬件复杂度之间的权衡
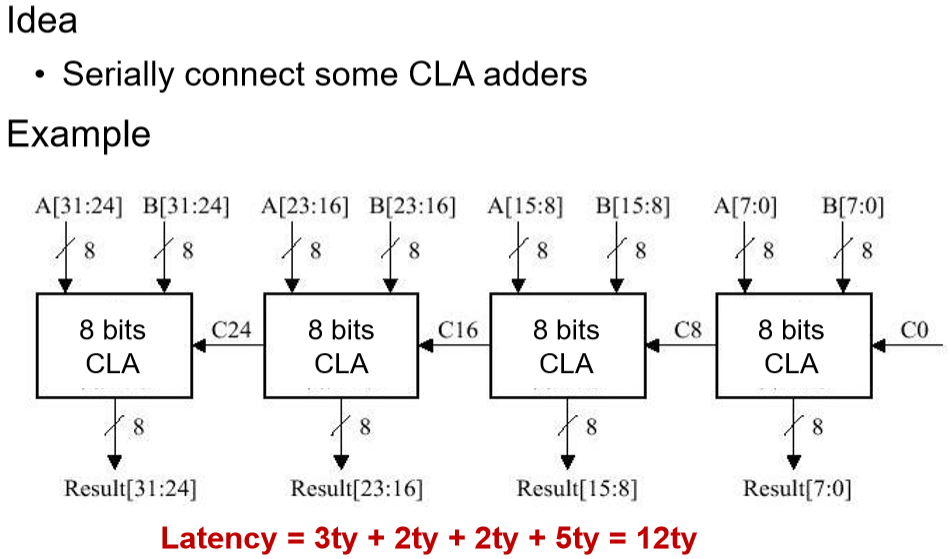
最后算出的是最前面的加法部分
最左边是3 = 1 + 2
然后中间两个+2:之前P和G都算好了
最后一步5 = 2 + 3
- P和G已经算好了
多一个加2
减法
$X - Y = X + (-Y)$
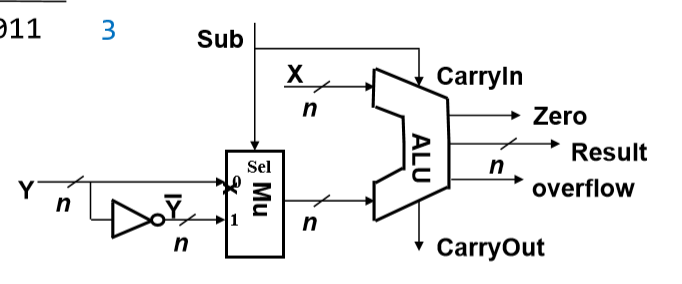
Sub是控制线,1为减法,0为加法
- Sub为1会走下面的路(取反)
Sub另一端连接在CarryIn上面
乘法
原码一位乘法
所有数用原码表示
计算X + Y:
符号位单独计算
X和Y数值位的绝对值进行计算
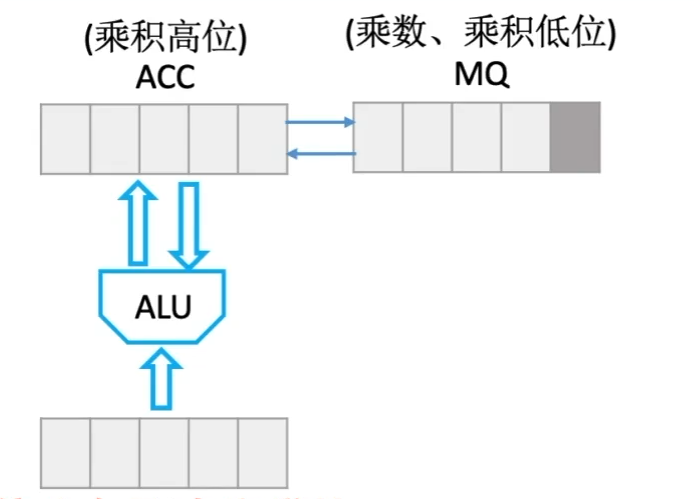
根据Y低位决定ACC
低位为1则ACC加X,然后逻辑右移
低位为0则ACC不变,然后逻辑右移
进行n次计算(X和Y的位数为n)
布斯乘法(补码一位乘法)
所有数用补码表示
计算 X + Y:
- 乘数末尾补0
这张图有问题,但是思想没问题
- 错误点是第三次横移应该高位补1

根据乘数最低两位决定ACC
最低位- 倒二低位 = 1:加上X补码,然后算数右移
最低位- 倒二低位 = 0:不变,然后算术右移
最低位- 倒二低位 = -1:加上-X补码,然后算术右移
进行n次运算(X和Y的位数为n)
除法
原码恢复余数法
所有数用原码表示
符号位单独处理
数值位采用绝对值计算
计算X / Y

根据$X + [-Y]_补$来计算
结果为负:上商0,加Y恢复余数,被除数和商左移一位
结果为非负:上商1,被除数和商左移一位
左移n次,上商n+1次(n为数值位)
- 最后一次不用左移
原码不恢复余数法
所有数用原码表示
符号位单独处理
数值位采用绝对值计算
计算X / Y
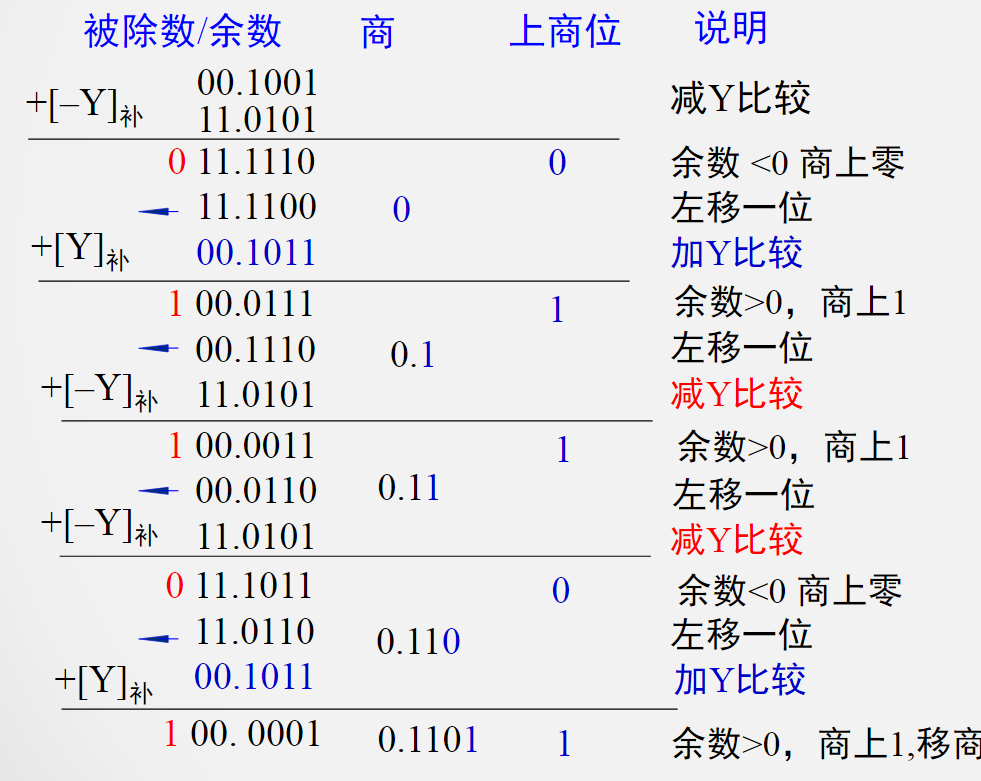
根据$X + [-Y]_补$来计算
结果为负:上商0,余数左移一位,再加Y
结果为非负:上商1,余数左移一位,再减Y
左移n次,上商n+1次(n为数值位)
最后一次不用左移
若最后一次余数为负,需要加Y得到正确的余数
补码不恢复余数法
所有数用补码表示
符号位参与运算
- 拓展为双符号位
计算X / Y
根据X和Y的符号来确定运算方式
同号:$X - Y$
异号:$X + Y$
根据余数和除数的符号来计算
同号:上商1,余数左移一位,然后再减Y
异号:上商0,余数左移一位,再加Y
左移n次,上商n+1次(n为数值位)
- 第n+1次上的商恒置为1
浮点数运算与表示
加法和减法
必须保证两个操作数有相同的指数值
$X_E \leq Y_E$
$X+Y = (X_S \times B^{X_E - Y_E} + Y_S) \times B^{Y_E}$
$X-Y = (X_S \times B^{X_E - Y_E} - Y_S) \times B^{Y_E}$
步骤:
检查0
对齐有效值
加或减有效值
规格化结果
原码加法
如果两个操作数有相同的符号,做加法;否则,做减法
做加法:直接相加
如果最高位有进位,则溢出
符号和被加数(被减数)相同
做减法:加第二个操作数的补数
如果最高位有进位,正确
- 符号与被减数相同
否则,计算它的补码
- 符号与被减数相反



乘法
无论哪个操作数是0,乘积都为0
从阶值的和中减去一个偏移量
- 其实是减去两个,但是最后表示出来要加一个
有效值相乘
结果规格化和舍入
- 规格化可能导致阶值下溢

除法
如果除数是0,则报告出错
如果被除数是0,则结果是0
被除数的阶值减除数的阶值,加上偏移量
有效值相除
结果规格化和舍入处理
精度考虑
寄存器的长度几乎总是大于有效值位长与一个隐含位之和,这些附加位称为保护位
- 保护位用0填充,用于扩充有效值的右端
舍入
四舍五入:结果被舍入成最近的可表示数
最后四位:如果第一位是0,直接截去
最后四位:如果第一位是1,产生进位
朝$\pm\infty$舍入:结果朝无穷大的方向舍入
朝0舍入:结果朝0舍入